gambar dari materi dan ulangan bab II

 (gb 2.1, 2.2, 2.3, 2.4, 2.5, 2.5, 2.6)



ULANGAN BAB II

1.Tentukan daerah penyelesaian dari pertidaksamaanpertidaksamaan berikut pada bidang koordinat cartesius.
a. x + 3y ≥ 6
b. 12x – 5y ≤ 60
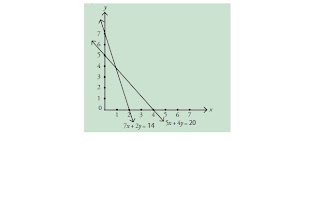
2.Tentukan daerah penyelesaian sistem per tidaksamaan linear berikut ini pada bidang koordinat cartesius.
a. 2x + y ≤ 6
x + 3y ≥ 9
x ≥ 0
y ≥ 0
b. 4x + 4y ≥ 163
x + 5y ≥ 157
x + 5y ≤ 35
x ≥ 0
y ≥ 0
3.Suatu lahan parkir memiliki luas 800 m2 dan hanya mampu menampung 64 bus dan mobil. Sebuah mobil menghabiskan tempat 6 m2 dan bus 24 m2. Biaya parkir Rp1.500,00/mobil dan Rp2.500,00/bus. Pemilik lahan parker mengharapkan penghasilan yang maksimum. Tentukan model matematika dari permasalahan tersebut.
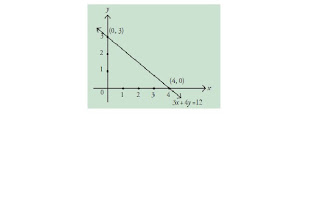
4.Tentukan nilai maksimum f(x, y) = 3x + 4y pada himpunan penyelesaian
sistem pertidaksamaan berikut.
x + 2y ≤ 10
4x + 3y ≤ 24
x ≥ 0
y ≥ 0