Program Linier
A. Sistem Pertidaksamaan Linear
1. Pertidaksamaan Linear Dua Variabel
Bentuk pertidaksamaan linear dua variabel sama dengan bentuk pertidaksamaan linear satu variabel, pertidaksamaan linear dua variabel memiliki dua variabel (peubah). Adapun pertidaksamaan linear satu variabel hanya memiliki satu peubah. Begitu pula dengan persamaan linear dua variabel sama dengan pertidaksamaan linear dua variabel, hanya saja berbeda dalam tanda ketidaksamaannya. Pada persamaan linear dua variabel, digunakan tanda hubung “ = ” sedangkan pertidaksamaan linear dua variabel digunakan tanda hubung “ >, <, ≥, atau ≤ “.
Definisi Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel adalah kalimat terbuka matematika yang memuat dua variabel, dengan masing-masing variabel berderajat satu dan dihubungkan dengan tanda ketidaksamaan. Tanda ketidaksamaanyang dimaksud adalah >, <, ≥, atau ≤.
Berikut bentuk umum dari pertidaksamaan linear dua variabel:
ax + by > c
ax + by < c
ax + by ≥ c
ax + by ≤ c
Dengan :
a = koefisien dari x, a ≠ 0
b = koefisien dari y, b ≠ 0
c = konstanta
a, b, dan c anggota bilangan real.
Untuk mengetahui manakah yang merupakan pertidaksamaan dengan melihat contoh dibawah ini
1. 2x < 15 4. x2 + 2y ≤ 5
2. 2x + 3y ≥ 6 5. –x ≥ y + 1
3. xy + x > 3
Manakah di antara pertidaksamaan-pertidaksamaan tersebut yang merupakan pertidaksamaan linear dua variabel? Dari ke lima nomor pertidaksamaan tersebut, yang merupakan pertidaksamaan linear dua variabel adalah pertidaksamaan nomor 2 dan 5. Pertidaksamaan nomor 1, merupakan pertidaksamaan linear satu variabel. Pertidaksamaan nomor 3 bukanlah pertidaksamaan linear dua variabel karena pada pertidaksamaan tersebut memuat perkalian variabel. Pertidaksamaan nomor 4 juga bukan pertidaksamaan linear dua variabel karena ada variabel yang derajatnya lebih dari satu. Penyelesaian dari suatu pertidaksamaan linear dua variabel berupa pasangan terurut (a, b) yang memenuhi pertidaksamaan linear dua variabel. Semua penyelesaian dari pertidaksamaan linear dua variabel disatukan dalam suatu himpunan penyelesaian. Himpunan penyelesaian dari suatu pertidaksamaan linear dua variabel biasanya disajikan dalam bentuk grafik pada bidang koordinat cartesius.
Langkah-langkah yang harus diambil untuk menggambarkan grafik penyelesaian dari per tidaksama an linear dua variabel, hampir sama dengan langkah-langkah dalam menggambarkan grafik persamaan linear dua variabel.
Berikut ini langkah-langkah mencari daerah penyelesaian dari pert idaksamaa n linear dua variabel.
a)Ganti tanda ketidaksamaan >, <, _, atau _ dengan tanda “ = “.
b)Tentukan titik potong koordinat cartesius dari persamaan linear dua variabel dengan kedua sumbu.
• Titik potong dengan sumbu x, jika y = 0 diapit titik (x,0)
• Titik potong dengan sumbu y, jika x = 0 diapit titik (0,y)
c)Gambarkan grafiknya berupa garis yang menghubungkan titik
(x,0) dengan titik (0,y). Jika pertidaksamaan memuat > atau <,gambar kanlah grafik tersebut dengan garis putus-putus.
d)Gunakanlah sebuah titik uji untuk menguji daerah penyelesaian pertidaksamaan.
e)Berikanlah arsiran pada daerah yang memenuhi himpunan penyelesaian pertidaksamaa n.
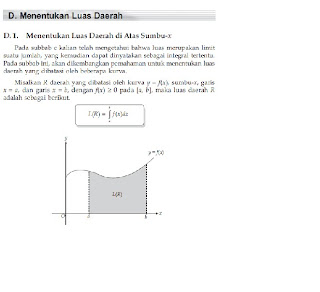
Gambarlah daerah himpunan penyelesaian pertidaksamaan
3x + 4y ≤ 12, x, y OER.
Jawab:
3x + 4y ≤12, ganti tanda ketidaksamaan sehingga diperoleh garis
3x + 4y =12.
• Titik potong dengan sumbu x, y = 0
3x + 4(0) = 12 3x = 12 x = 4
Titik potong dengan sumbu y, x = 0
3(0) + 4y = 12 3x = 12 y = 3
(GB 2.1)
• Titik potong dengan sumbu koordinat di (4, 0) dan (0, 3). Diperoleh grafi k 3x + 4y =12. Ambil titik uji (0, 0) untuk mendapatkan daerah penyelesaian dari pertidaksamaan 3x + 4y ≤12 , diperoleh 3(0) + 4(0) ≤ 12 0 ≤ 12 (Benar)
Dengan demikian, titik (0, 0) memenuhi pertidaksamaan 3x + 4y ≤ 12. Himpunan penyelesaian pertidaksamaan adalah daerah di bawah garis batas
(yang diarsir).
(GB 2.2)
2. Sistem Pertidaksamaan Linear Dua Variabel
Jika memiliki dua atau lebih pertidaksamaan linear dua variabel, dan pertidaksamaan tersebut saling berkaitan maka terbentukl ah suatu sistem. Sistem inilah yang dinamakan sistem per tidaksamaan linear dua variable.
Definisi Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel adalah suatu sistem yang terdiri atas dua atau lebih pertidaksamaan dan setiap pertidaksamaan tersebut mem punyai dua variabel.
Langkah-langkah menentukan daerah) penyelesaian dari system pertidaksamaan linear dua variabel sebagai berikut.
a)Gambarkan setiap garis dari setiap pertidaksamaan linear dua variabel yang diberikan dalam sistem pertidaksamaan linear dua variabel.
b)Gunakanlah satu titik uji untuk menentukan daerah yang memenuhi setiap pertidaksamaan linear dua variabel. Gunakan arsiran yang berbeda untuk setiap daerah yang memenuhi pertidaksamaan yang berbeda.
c)Tentukan daerah yang memenuhi sistem pertidaksamaan linear, yaitu daerah yang merupakan irisan dari daerah yang memenuhi pertidaksamaan linear dua variabel pada langkah b.
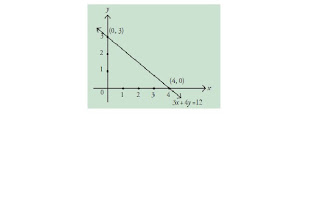
Tentukan daerah penyelesaian dari sistem pertidaksamaan linear berikut.
5x + 4y 20
7x + 2y 14
x 0
y 0
Jawab:
Gambarkan setiap garis batas dari sistem pertidaksamaan linear dua variabel,
yaitu 5x + 4y = 20, 7x + 2y = 14, x = 0 (sumbu y), y = 0 (sumbu x).
(GB 2.3
Gunakan titik uji (0, 0) pada setiap pertidaksamaan linear dua variabel
yang diberikan
• 5x + 4y 20
5(0) + 4(0) 20
0 20 (memenuhi)
Daerah yang memenuhi berada di sebelah kiri garis 5x + 4y = 20
• 7x + 2y 14
7(0) + 2(0) 14
0 14 (memenuhi)
Daerah yang memenuhi berada di sebelah kiri garis 7x + 2y = 14
• x 0 dan y 0
Daerah yang memenuhi berada di kuadran I.
Dengan pola yang berbeda, arsirlah (raster) setiap daerah yang memenuhi setiap pertidaksamaan linear dua variabel tersebut, seperti ditunjukkan pada gambar berikut.
(GB 2.4)
Jika garis batas yang akan diberikan pada daerah penyelesaian system pertidaksamaan linear memotong sumbu koordinat-x dan koordinat-y dititik (b, 0) dan (0, a) maka persamaan garisnya adalah Jika garis batas diberikan pada daerah penyelesaian system pertidaksamaan linear melalui titik (x1, y1) dan (x2, y2) maka persamaan garisnya adalah
atau ax + by = ab
y – y1 = m (x – x1) dengan m
Jika garis batas diberikan pada daerah penyelesaian system pertidaksamaan linear melalui titik (x1, y1) dan (x2, y2) maka persamaan garisnya adalah
y – y1 = m (x – x1) dengan atau
ini digunakan jika sebuah gambar grafik diketahui untuk mencari pertidak samaan.
SELAMAT BELAJAR
LATIHAN SOAL
1.Buatlah 2 contoh sistem pertidaksamaan linear duavariabel. Kemudian, tentukan daerah penyelesaiannya pada bidang koordinat cartesius.
2.Buatlah 2 contoh daerah penyelesaian sistem pertidaksamaan linear dua variabel (pada koordinat cartesius). Kemudian, tentukanlah sistem pertidaksamaan linear dua variabel yang memenuhi daerah penyelesaian tersebut.
3.Tentukan daerah penyelesaian dari pertidaksamaanpertidaksamaan
berikut pada bidang koordinat cartesius.
a. 6x – 5y < 30
b.–2x – 3y < –6.000
4.Seorang pemborong pengecatan rumah mempunyai persediaan 80 kaleng cat berwarna putih dan 60 kaleng cat berwarna abu-abu. Pemborong tersebut mendapat tawaran untuk mengecat ruang tamu danruang tidur. Setelah dihitung, ternyata 1 ruang tamu menghabiskan 2 kaleng cat putih dan 1 kaleng cat abu-abu, sedangkan 1 ruang tidur menghabiskan 1 kaleng cat putih dan 1 kaleng cat abu-abu. Jika banyak ruang tamu x buah dan banyaknya ruang tidur y buah, dapatkah Anda menentukan system pertidaksamaan dari permasalahan tersebut?
Program Linier
B.Program Linier
1.Model Matematika
Misalnya, dalam menjalani proses produksi pada suatu perusahaan, pastilah tersedia bahan baku, tenaga kerja, mesin, dan sarana produksi lainnya. Seorang pengusaha harus memperhitungkan semua faktor yang ada supaya perusahaannya dapat meminimumkan biaya produksi dan memaksimumkan keuntungan yang diperoleh. Program linear dapat digunakan untuk menyelesaikan masalahmasalah
tersebut. Akan tetapi, masalah-masalah tersebut terlebih dahulu harus diterjemahkan ke dalam bahasa matematika sampai ke tingkat yang paling sederhana. Proses menterjemahkan masalah nyata ke dalam bahasa matematika dinamakan pemodelan matematika.
Misalkan seorang agen sepeda ingin membeli paling banyak 25 buah sepeda untuk persediaan. Ia ingin membeli sepeda model biasa dengan harga Rp1.200.000,00/buah dan sepeda model sport dengan harga Rp1.600.000,00/buah. Ia mempunyai modal Rp33.600.000,00. Ia berharap memperoleh untung Rp200.000,00 untuk setiap sepeda biasa dan Rp240.000,00 untuk setiap sepeda sport. Jika Anda diminta untuk memodelkan masalah ini, dengan harapan agen sepeda tersebut mendapatkan keuntungan maksimum, dapatkah Anda membantunya? Untuk memodelkan permasalahan tersebut, langkah pertama dimulai dengan melakukan pemisalan. Pada permasalahan tersebut, ada 2 model sepeda yang ingin dibeli oleh agen, yaitu sepeda biasa dan sepeda sport. Misalkan banyaknya sepeda biasa yang dibeli adalah x buah dan banyaknya sepeda sport yang dibeli adalah y buah. Oleh karena keuntungan yang diharapkan dari sepeda biasa dan sport berturut-turut adalah Rp200.000,00 dan Rp240.000,00 maka keuntungan yang mungkin diperoleh agen tersebut ditentukan oleh z = f(x, y) = 200.000x + 240.000y
Fungsi z = f(x, y) tersebut dinamakan sebagai fungsi objektif (fungsi tujuan). Dari permasalahan yang ada, diinginkan untuk memaksimumkan keuntungan yang didasarkan pada kondisi-kondisi yang ada (kendala). Setiap kendala yang ada, bentuknya berupa pertidaksamaan. Fungsi kendala dari permasalahan agen sepeda tersebut ditentukan sebagai berikut:
• Banyaknya sepeda yang akan dibeli oleh agen tersebut
x + y ≤ 25
• Besarnya modal yang dimiliki agen sepeda
1.200.000x + 1.600.000y ≤ 33.600.000
15x + 20y ≤ 42
• Banyaknya sepeda yang dibeli tentu tidak mungkin negatif sehingga
nilai x ≥ 0 dan y ≥ 0.
Dengan demikian, terbentuklah model matematika berikut.
z = f(x, y) = 200.00x + 240.000y
Tujuannya memaksimumkan fungsi tujuan yang didasarkan pada kondisi
x + y ≤ 25
15x + 20y ≤ 42
x ≥ 0
y ≥ 0.
Model matematika dari setiap permasalahan program linear secara umum terdiri atas 2 komponen, yaitu:
1. Fungsi tujuan z = f(x, y) = ax + by dan
2. Fungsi kendala (berupa pertidaksamaan linear)
SELAMAT BELAJAR
LATIHAN SOAL
1)Apakah yang dimaksud dengan model matematika?
Jelaskan dengan menggunakan kata-kata sendiri.
2)Apa yang Anda ketahui tentang program linear?
3)Harga 1 kg beras Rp6000,00 dan 1 kg gula Rp4500,00. Seorang pedagang memiliki modal Rp500.000,00 dan tempat yang tersedia hanya memuat 1 kuintal. Jika pedagang tersebut membeli x kg beras dan y kg gula, tentukan model dari masalah tersebut.
4)Tanah seluas 10.000 m2 akan dibangun rumah tipe A dan tipe B. Untuk rumah tipe A diperlukan 100 m2 dan tipe B seluas 75 m2, rumah yang akan dibangun paling banyak 125 unit. Keuntungan rumah tipe A Rp 6.000.000,00/unit dan tipe B Rp 4.000.000,00/unit. Keuntungan maksimum yang dapat diperoleh dari penjualan rumah tersebut adalah ....
Program Linier
1.Masalah Program Linear
Program linear akan sangat berguna bagi Anda ketika dihadapkan pada beberapa pilihan dengan kendala-kendala tertentu, yang menuntut. Anda untuk mengambil keputusan yang optimum (maksimum atau minimum). Oleh karena itu, permasalahan dalam program linear selalu berhubungan denga pengoptimalisasian fungsi tujuan berdasarkankendala yang membatasinya.
Suatu program linear dua variabel x dan y memiliki satu fungsi tujuan
yang dioptimumkan. Bentuk umum dari fungsi tujuan tersebut adalah sebagai berikut.
z = f(x, y) = ax + by dengan a, b bilangan real, a ≠ 0 dan b ≠ 0
Pada Contoh Soal 1.9 , fungsi tujuan yang ingin dimaksimumkan adalah z = f(x, y) = 1.500x + 1.250y, dan fungsi kendalanya adalah
x + y ≤ 60
2.500x + 2.000y ≤ 140.000
x ≥ 0
y ≥ 0
Tujuan dari permasalahan tersebut adalah menentukan banyaknya buah semangka dan melon yang harus dibeli/disediakan agar diperoleh keuntungan maksimum.
Dalam memaksimumkan suatu fungsi tujuan z = ax + by, Anda perlu menentukan titik-titik (x, y) yang menghasilkan nilai z terbesar. Titik (x, y) yang menghasilkan nilai z terbesar harus memenuhi setiap pertidaksamaan linear pada fungsi kendala yang diberikan. Hampir sama dengan hal itu, dalam meminimumkan suatu fungsi, Anda perlu menentukan titik-titik (x, y). Namun dalam meminimumkan fungsi tujuan, dicari titik (x, y) yang menghasilkan nilai z terkecil. Berdasarkan uraian tersebut, diketahui bahwa model matematika yang diperoleh pada Contoh Soal 1.9 merupakan contoh permasalahan dalam upaya memaksimumkan fungsi tujuan.Dengan demikian, masalah program linearnya sebagai berikut. Fungsi tujuan z = f(x, y) = 1.500x + 1.250y dengan kendalanya adalah
x + y ≤ 60
2.500x + 2.000y ≤ 140.000
x ≥ 0
y ≥ 0
(GB 2.5)
Dengan menggunakan konsep sistem pertidaksamaan linear dua variabel, diperoleh daerah penyelesaian seperti pada gambar berikut:
(GB 2.5)
Dengan menggunakan konsep sistem pertidaksamaan linear dua variabel, diperoleh daerah penyelesaian seperti pada gambar berikut.
Selanjutnya, cari koordinat titik C yang merupakan perpotongan antara garis x + y = 60 dan 2.500x + 2.000y = 140.000. Gunakan metode gabungan eliminasi dan substitusi
x + y = 60 | × 2.000| 2.000x + 2.000y = 120.000
2.500x + 2.000y = 14.000 |× 1 | 2.500x + 2.000y = 140.000 – 500x = –20.000
x = 40
Substitusikan nilai x = 40 ke persamaan x + y = 60 diperoleh
40 + y = 60
y = 60 – 40
y = 20
Jadi, koordinat titik C adalah (40, 20).
Dari permasalahan ini diketahui koordinat titik sudut daerah penyelesaian dari sistem tersebut adalah A(0, 60), B(56, 0), C(40, 20) dan O(0, 0). Oleh karena tujuan dari permasalahan ini adalah ingin memaksimumkan nilai z maka tentukan dari keempat titik tersebut yang membuat nilai z maksimum, dengan cara menyubstitusikannya ke fungsi z = f(x, y) = 1.500x + 1.250y. Untuk A (0, 60) maka
z = 1.500(0) + 1.250(60) = 75.000
• Untuk B (56, 0) maka
z = 1.500(56) + 1.250(0) = 84.000
• Untuk C (40, 20) maka
z = 1.500(40) + 1.250(20) = 85.000
• Untuk O (0, 0) maka
z = 1.500(0) + 1.250(0) = 0
Fungsi z maksimum di titik C (40, 20) dengan z = 85.000.
Metode yang Anda gunakan pada uraian tersebut dikenal sebagai metode titik sudut. Secara umum, langkah-langkah dalam menentukan
nilai optimum masalah program linear dengan fungsi tujuan z = f(x, y) = ax + by
Menggunakan metode titik sudut adalah sebagai berikut:
1.Buat model matematika dari masalah program linear yang diberikan.
2.Gambarkan grafi k-grafi k dari setiap pertidaksamaan linear dua variabel yang diketahui.
3.Tentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linear dua variabel yang terdapat pada masalah (irisan dari setiap pertidaksamaan linear dua variabel yang diberikan).
4.Tentukan titik-titik sudut pada daerah himpunan penyelesaiannya.
5.Substitusikan titik-titik sudut tersebut ke dalam fungsi tujuan. Ambil nilai yang paling besar untuk penyelesaian maksimum, atau ambil nilai yang paling kecil untuk penyelesaian minimum. Titik yang memberikan nilai optimum (maksimum atau minimum) dinamakan titik optimum.
Seorang anak penderita kekurangan gizi diharuskan makan dua jenis tablet
vitamin setiap hari. Tablet pertama mengandung 5 unit vitamin A dan 3
unit vitamin B, sedangkan tablet kedua mengandung 10 unit vitamin A
dan 1 unit vitamin B. Dalam satu hari, anak itu memerlukan 20 unit
vitamin A dan 5 unit vitamin B. Jika harga tablet pertama Rp400,00/biji
dan tablet kedua Rp600,00/biji, tentukan pengeluaran minimum untuk
pembelian tablet per harinya.
Jawab:
Permasalahan tersebut dapat disajikan dalam tabel berikut.
Tabel1
Tabel2
Vitaman A
5
10
Vitaman B
3
1
Misalkan, banyaknya tablet 1 sebanyak x biji dan tablet 2 sebanyak y biji. Model matematika untuk masalah tersebut adalah sebagai berikut. Fungsi tujuan:
z = f (x, y) = 400 x + 600 y
Kendala:
5x + 10y ≥ 20
3x + y ≥ 5
x ≥ 0
y ≥ 0
Berdasarkan model matematika tersebut, diperoleh daerah himpunan
penyelesaiannya seperti pada gambar berikut.
(GB 2.6)
Titik B adalah koordinat titik potong garis 5x + 10y = 20 dan 3x + y = 5.
Untuk mendapatkan titik B, cari penyelesaian dari kedua garis tersebut.
5x + 10y = 20 | ×1 | 5x + 10y = 20
3x + y = 5 |×10 | 30x + 10y = 50
-
–25x = – 30
x =
subtitusikan nilai x = ke persamaan 3x + y = 5, diperoleh
3() + y = 5
y = 5 -
y = y =
Titik-titik sudut yang terdapat pada daerah himpunan penyelesaian tersebut adalah A (4, 0), Bdan C(0,5). Nilai fungsi tujuan dari ketiga titi k ter s ebut disajikan dalam tabel berikut.
Titik sudut
Z=f(x,y)= 400x + 600y
A(4, 0)
1.600
1.320
C(0, 5)
3.000
Jadi, nilai minimum untuk fungsi tujuan tersebut adalah 1.320. Artinya pengeluaran minimum untuk pembelian tablet per harinya Rp1.320,00.
LATIHAN SOAL
1.Suatu lahan parkir memiliki luas 800 m2 dan hanya mampu menampung 64 bus dan mobil. Sebuah mobil menghabiskan tempat 6 m2 dan bus 24 m2. Biaya parkir Rp1.500,00/mobil dan Rp2.500,00/bus. Pemilik lahan parker mengharapkan penghasilan yang maksimum. Tentukan model matematika dari permasalahan tersebut.
2.Nilai maksimum dari f(x, y)= 10x + 20y dengan kendala x ≥ 0, y ≥ 0,x + 4y ≤ 120, x + y ≤ 60 adalah….
3.Cokelat A yang harganya Rp600,00 per bungkus dijual dengan laba Rp80,00 per bungkus. Cokelat B harganya Rp1.000,00 per bungkus dijual dengan laba Rp125,00 per bungkus. Modal yang dimiliki pedagang adalah Rp300.000,00 dan kotak tempat menjual cokelat mampu memuat 350 bungkus. Tentukan:
a. laba maksimum yang dapat diperoleh pedagang,
b. banyaknya cokelat A dan cokelat B yang harus dibeli pedagang agar dapat diperoleh laba yang maksimum.